BOYLE’S LAW

BOYLE’S LAW

According to this law, for a given sample of a gas, the pressure is inversely proportional to its volume at constant Temperature. That is, if we increase the volume then the pressure decreases and vice-versa. This is obvious as on increasing volume the contact area increases and that’s why pressure decreases. The force remains the same as the temperature is constant.(BOYLE’S LAW).

P ά 1/V

PV = constant

P₁V₁ = P₂V₂ = P₃V₃

If the pressure is doubled, the volume is halved. If the pressure is halved, the volume is doubled.

The study of graphs plays a vital role in understand these laws.

The P-V graph is called “rectangular hyperbola” as it represents a standard curve which follows the equation xy = constant.

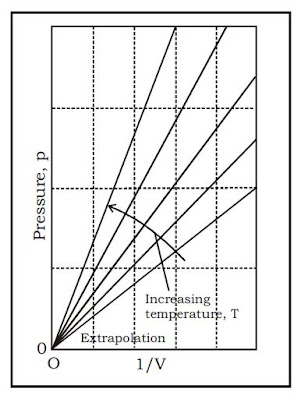
Straight lines are obtained when the pressure is plotted against 1/V at constant temperature.

The P-V graph is called “rectangular hyperbola” as it represents a standard curve

which follows the equation xy = constant. As they are drawn at constant T, these curves are also called “Isotherms”.

Experiments of Boyle, in a quantitative manner prove that gases are highly

compressible because when a given mass of a gas is compressed, the same number of molecules occupy a smaller space. This means that gases become denser at high pressure.

A relationship can be obtained between density and pressure of a gas by using Boyle’s law . By definition, density ‘d’ is related to the mass ‘m’ and the volume ‘V’ by the relation  d = m / V. If we put value of V in this equation from Boyle’s law equation, we obtain the relationship.

d ={m/k}P =K' P

This shows that at a constant temperature, pressure is directly proportional to the density of a fixed mass of the gas.

Example : A balloon is filled with hydrogen at room temperature. It will burst if pressure exceeds 0.2 bar. If at 1 bar pressure the gas occupies 2.27 L volume, upto what volume can the balloon be expanded ?

Solution

According to Boyle’s Law P1V1 = P2V2

If P1 is 1 bar, V1 will be 2.27 L

If P2 = 0.2 bar, then

V2 = 1 bar x  2.27 x 1/0.2  = 11.35L

Since balloon bursts at 0.2 bar pressure, the volume of balloon should be less than 11.35 L.

Example:

A 1.00 L sample of gas at 760 torr is compressed to 0.800 L at constant temperature. Calculate the final pressure of the gas.

Solution. P₁V₁ = P₂V₂

(760) (1) = P₂ (0.8)

P₂ = 950 torr

Applications of Boyle's Law

1. Scuba Diving/Deep Water Diving

                                          Back to chemistry notes