CHARLES LAW
CHARLES LAW:According to this law, the volume
of a sample of a gas is directly proportional to its absolute Temperature (in
K) at constant pressure. On increasing the Temperature the kinetic energy of
the molecules increases, so they collide with the walls with greater force and
because we are keeping the pressure constant this greater force results in
increase of volume of the sample.
V/T = constant V = kT
V1/T1 = V2/T2 = V3/T3 = ....so on
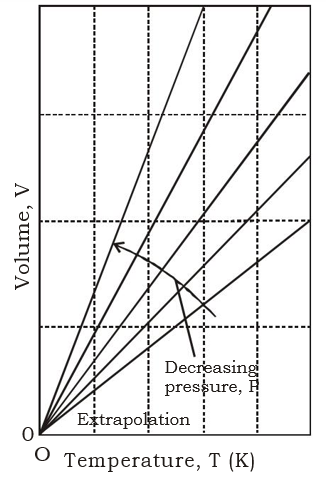
The variation of the volume of a
fixed amount of gas with the temperature at constant pressure. Note that in
each case the isobars extrapolate to zero volume at T = 0, or q = –273°C.
The V-T graph obtained is a
straight line passing through origin as it represents the equation y = mx where
m is the slope of the line. At 0 K the volume also becomes almost zero. The
graph is extrapolated/dotted because this condition is unattainable. However,
when the same graph is drawn with Temperature in 0C then the curve shifts
and it intersects the x-axis at -273.150C as shown. These graphs are
called “isobars”(constant pressure
curves).
We can see that the volume of the gas at – 273.15 °C ( 0 K) will be zero.
This means that gas will not exist. In fact all the gases get liquefied
before this temperature is reached. The lowest hypothetical or
imaginary temperature at which gases are supposed to occupy
zero volume is called Absolute zero. All gases obey Charles’ law
at very low pressures and high temperatures.
Q. A sample of gas at 1.20 atm and
27°C is heated at constant pressure to 57°C. Its final volume is 4.75 L. What
was its original volume?
Solution.
P1 = P2 = 1.2 atm
V1 =? V2 = 4.75L
T1= 300K T2 = 330 K
From Charles’ law:
V1 = V2
T1
T2
V1 = 4.32L